Jeux d'esprit
Allumettes
8 triangles
Comment obtenir 8 triangles équilateraux avec 6 alumettes ?
- Réponse
On fait une étoile de David (6 petits triangles formés par chaque pointe et 2 grands tête-bêches).
(Merci Solidsteak02)
5 carrés identiques
Nous avons 5 carrés identiques.

A vous d'en faire 4 en ne deplacant que 3 allumettes.
Attention, les grands carrés formés de plusieurs petits comptent aussi.
- Réponse
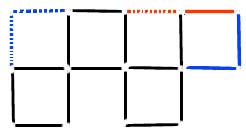
(Merci Minouchou)
L'olive et le verre
La figure ci dessous représente une olive au fond d'un verre.

Pouvez vous faire sortir l'olive du verre en ne déplacant que 2 allumettes ?
- Réponse
1. 0n déplace un peu l'allumette horizontale
2. Puis l'allumette verticale de droite.
-> On trouve un verre renversé, l'olive est à l'extérieur.
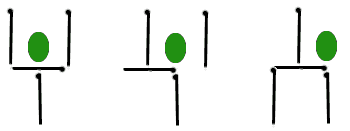
(Merci Fred)
2 rectangles égaux

Quelles allumettes allez vous retirer pour que cette figure formant 6 carrés se transforme en 2 rectangles ?
- Réponse
-
Il faut enlever les 4 allumettes verticales qui sont au milieu.
On a ainsi deux rectangles horizontaux l'un au dessus de l'autres de 3 allumettes de long.
(Merci Bernard, Golgot59, Phil et Anh Minh)
Enlever les trois allumettes horizontales de la colonne du centre. Ainsi il y a rectangles de deux carrés de haut.
(Merci castalie)
Obtenir 139
En deplacant une seule allumette de l'equation ci dessous, serez vous capable d'obtenir 139 ?
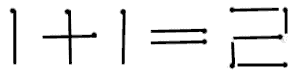
- Réponse
Prendre une allumette qui forme le signe = et la placer contre le signe plus pour dessiner un 4.
On peut alors lire 141 - 2, ce qui vaut bien 139 !
(Merci Romain)
Former un carré
Pouvez vous former un carré avec seulement 3 allumettes ?
- Réponse
-
Ecrire le nombre 1. 1 est le carré de 1.
Ou écrire 4 qui est le carré de 2.
(Merci Romain)
Ecrire le nombre IX (9 en chiffre romain) qui est le carré de 3.
(Merci Matmer)
IL en chiffres roamins = 7 x 7
(Merci Fanfan78)
Ecrire un C qui correspond en chiffres romains à 100 qui est le carre de 10.
(Merci Fredouy)
Deux alumettes plantées verticalement dans le sol et une reposant en équilibre dessus. Avec le sol ça fait un carré.
(Merci Bmstratetj)
En cassant les allumettes.
(Merci Jordan)
Les 3 carrés
Ces 12 allumettes composent 4 carrés (ou 5 si l'on veut...).
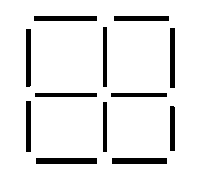
Déplacez 3 allumettes de facon à obtenir 3 carrés.
- Réponse
Sur deux "étages" :
1er étage : un carré, l'espace d'un carré, un autre carré.
2ème étage : un carré au niveau de l'espace du premier étage.
On peut bien sur faire des figures symétriques.
(Merci Lili_au_secour)
4 carrés
La figure est realisée à partir d'allumettes.

Comment obtenir quatres carrés de même taille en DEPLACANT uniquement DEUX de ces allumettes ?
Indice 1
Indice 2
- Réponse
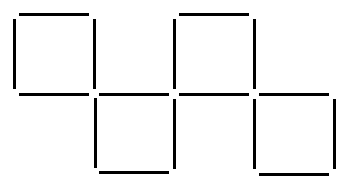
(Merci Romain)
Une addition
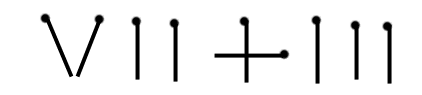
Comment obtenir 8 en changeant une seule allumette de place dans cette addition ?
Indice 1
- Réponse
-
V + I + II
On prend l'allumette tout à droite et on transforme le VII en V + I.
(Merci Fredouy)
On transforme le VII en VI et on transforme le III en I + I
VI + I + I
(Merci Dexterpumba)
Je transforme le 1er "I" en "/" et j'obtiens : V/I (5 divisé par 1 = 5), je laisse "+III". Ce qui me donne: V/I+III (5+3=8).
(Merci Jimmp)
Une équation
V|| = |
Bouger une seule allumette sans toucher au signe "egal" pour obtenir une égalité.
Indice 1
Indice 2
Indice 3
- Réponse
Tourner le 2ème "I" de VII pour écrire V~ (= racine de) 1 = 1
(Merci Romain)
Une autre équation
|=||
Bouger une allumette sans toucher au signe "=" pour obtenir une egalité.
- Réponse
-
| = | ' (On décale la dernière allumette vers le haut pour en faire une puissance).
(Merci LightSlasher)
On colle les deux allumettes de droites pour faire un | plus épais.
(Merci Bardan)
= |-| ( 0 = 1 - 1)
Bien sur si 0 est équivalent à rien.
(Merci Brownast)
Ecrire 1 congru à 1 ne fonctionne pas (il faudrait indiquer le modulo).
Déplacer une allumette du II pour la transformer en barre du 1 ne fonctionne pas bien non plus car elle sera trop longue.
Une infinité de triangles
Comment construire une infinité de triangles avec seulement 6 allumettes ?
Indice 1
Indice 2
Indice 3
- Réponse
-
Former un triangle isocèle avec 3 allumettes puis ajouter les médianes avec les trois autres.
Cela fait déjà un bon nombre de triangles.
Ou, avec un jeu de mot approximatif, tracer le signe infini sous la forme de 2 triangles opposés par la pointe, comme un huit couché.
(Merci Romain)
Avec des miroirs.
(Merci Nic)

