Jeux d'esprit
Casse-tête
Traverser le pont
4 personnes sont au bout d'un pont et veulent le traverser.
Pour cela ils ont besoin obligatoirement d'une lanterne (ils n'en possedent qu'une) et ne peuvent traverser qu'à deux en même temps.
Ces 4 personnes ne sont pas toutes aussi rapides. Elles peuvent traverser respectivement en 1, 2, 5 et 10 minutes.
Bien sur quand deux personnes traversent ensemble, la plus rapide va au meme rythme que l'autre.
Comment faire pour faire traverser toutes ces personnes en exactement 17 minutes ?
- Réponse
1°) On fait traverser celui qui traverse en 1mn et celui qui traverse en 2mn. (+2mn)
2°) On fait revenir celui qui traverse en 1mn. (+1mn)
3°) On fait traverser celui qui traverse en 10mn et celui qui traverse en 5mn. (+10mn)
4°) On fait revenir celui qui traverse en 2mn. (+2mn)
5°) On fait traverser celui qui traverse en 1mn et celui qui traverse en 2mn. (+2mn)
TOTAL : 17mn
Les 2 jarres
Vous devez donner à un grand sage exactement 4 litres d'eau pour qu'il vous raconte le commencement du monde.
Pour cela, vous ne disposez que de deux jarres : la première de 5 litres et la deuxième de 3 litres.
Comment allez-vous vous y prendre ?
Indice 1
Indice 2
Indice 3
- Réponse
-
1) Remplir la jarre de 5L et la vider dans celle de 3L.
2) Vider la jarre de 3L et y transvaser les 2L restant dans celle de 5L.
3) Remplir la jarre de 5L puis transvaser dans celle de 3L le litre nécessaire pour finir de la remplir.
(Merci Pierrot, Lotfi, Bigbabar, Shadow, Barinois, Bierre, Bekkaye, @ir1, Choukir, Djteubai, Matethieu, Zolrich)
1) Remplir celle de 3L et la vider dans celle de 5L.
2) Remplir celle de 3L et la vider dans celle de 5L jusqu'à ce qu'elle soit pleine.
3) Vider celle de 5L et la remplir avec le 1L qui restait dans celle de 3L.
4) Remplir celle de 3L et la vider dans celle de 5L.
(Merci Jhbfklgs)
Les 3 ampoules
Tu es dans une pièce possedant 3 interrupteurs reliés a 3 ampoules situées dans une autre pièce.
Tu dois savoir quel interrupteur allume quelle ampoule en n'allant qu'une fois dans la pièce aux ampoules, tout en sachant que les deux pièces sont séparées par un sas hermetiques à la lumilière. et qu'il est donc impossible depuis la première pièce de savoir si les ampoules sont allumées dans l'autre pièce.
Indice 1
Indice 2
Indice 3
Indice 4
- Réponse
1)Allume le 1er interrupteur.
2)Au bout de 5mn, éteint le, allume le 2ème et va dans la pièce.
3) Le premier interrupteur commande l'ampoule qui est éteinte et chaude.
Le second commande celle qui est allumée.
Le troisième commande la dernière.
Les 3 missionnaires
Trois missionaires et trois cannibal doivent traverser une rivière.
Les trois missionnaires et un cannibal savent ramer.
Ils ont une barque de 2 personnes.
S'il y a d'un coté ou d'un autre de la rivière un nombre supérieure de cannibales que de missionnaires, les missionnaires se font manger.
N'oublier pas de ramener la barque, personne ne doit se faire manger...
Indice 1
Indice 2
Indice 3
- Réponse
Il y a plusieurs solutions. En voici une :
Soit M Missionnaire, C Canibale non rameur, R Canibale rameur, \/ la barque et ~~~ la rivière.
M-M-M-R-C-C-\/~~~
M-M-M-C~~~R-C-\/
M-M-M-R-C-\/~~~C
M-M-M~~~R-C-C-\/
M-M-M-R-\/~~~C-C
M-R~~~M-M-C-C-\/
M-M-R-C-\/~~~M-C
M-C~~~M-M-R-C-\/
M-M-C-C-\/~~~M-R
C-C~~~M-M-M-R-\/
R-C-C-\/~~~M-M-M
C~~~M-M-M-R-C-\/
R-C-\/~~~M-M-M-C
~~~M-M-M-R-C-C-\/
Les 8 pions
Ce problème se traite avec 8 pions et un damier de 8*8 (un échiquier).
Il faut placer les 8 pions sur le damier de façon qu'aucun d'eux ne se trouve dans la même rangée, colonne ou diagonale.
Vous avez trouvez une solution ? Alors maintenant essayer de faire en sorte qu'il n'y ait pas trois pions alignés dans n'importe quelle direction.
Indice 1
Indice 2
Indice 3
- Réponse
- - - - - - O -
- O - - - - - -
- - - O - - - -
O - - - - - - -
- - - - - - - O
- - - - O - - -
- - O - - - - -
- - - - - O - -
(Merci Marine)
10 pièces
Vous avez 10 pieces de monnaies et devez faire deux rangées de 5 et 6 pièces, comment vous y prenez vous ?
- Réponse

La 3ème flèche
En seulement 2 coups de crayon supplémentaires, est il possible de faire une 3ième flèche (formée d'un seul bloc) sur le dessin ci dessous ?

- Réponse

(Merci Soulard5 et Orel)
Faire un 6
Avec çà :

Essayez de faire un 6, en rajoutant un trait, sans lever le crayon.
(Recopiez sur une feuille si vous le voulez. Vous êtes libre...)
Indice 1
Indice 2
Indice 3
- Réponse
-
S+IX=>SIX
IX6 (un multiplié par 6 = 6)
(Merci Eros, Rachel et Tite-jeanne-xd)
Les 6 clous
Comment faire tenir 6 clous à tête plate sur un seul autre clou ?
Indice 1
Indice 2
- Réponse
-
Pincer les têtes de 4 clous alignés entre deux clous parallèles et tête bêche.
Ecarter la pointe des clous 1 et 3 d'un côté et des clous 2 et 4 de l'autre en forme de toit.
Poser l'assemblage sur la tête du premier clou.
Cela devrait tenir, mais c'est plus stable avec 8 clous !
(Merci Romain)
On pose à plat le premier clou ... et on pose tranquillement les 6 autres clous sur ce premier...
cqfd :-)))
(Merci Oli)
9 moutons malades
9 moutons sont dans un prés carré mais ils sont malades.
Le but de la maneuvre est de les isoler en utilisant seulement deux carrés.
Les x représentent les moutons:
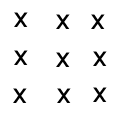
Indice 1
Indice 2
- Réponse

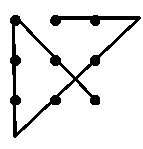
Les 9 points
Comment dessiner une ligne brisée continue de 4 segments qui passe une fois et une seule par chacun de ces 9 points ?
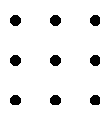
Indice 1
Indice 2
Indice 3
- Réponse
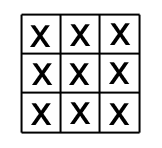
Le carré magique
Placez les chiffres 1,2,3,4,5,6,7,8,9 dans la grille suivante de manière à ce que la somme des chiffres de chaque ligne, chaque colonne, et chaque diagonale soit égale à 15.
- Réponse
Il y a plusieurs solutions plus ou moins symétriques. En voici une :
2 7 6
9 5 1
4 3 8
Des crayons
Comment disposer 6 crayons pour qu'ils soient tous en contact entre eux ?
Indice 1
Indice 2
Indice 3
- Réponse
-

(Merci Tarasboulba)
En les faisant se toucher par la pointe.
(Merci Lilissia et Anouck)
La fontaine
Il y a une fontaine carrée, et à chaque coin de cette fontaine pousse un arbre.
Comment doubler la superficie de la fontaine, en maintenant sa forme carrée sans couper d'arbres ?

- Réponse

Le loup, la chèvre et le chou
Un fermier accompagné d'une chèvre, d'un loup et d'un choux doit traverser une rivière pour rentrer chez lui.
Malheureusement, il ne possède qu'une minuscule barque ne lui permettant de transporter qu'un seul de ses "compagnon" à la fois.
Ainsi, à chaque aller-retour, il doit en laisser deux sans surveillance le temps de faire le voyage.
Comment va-t-il s'y prendre pour tous les faire traverser, sans qu'aucun ne se fasse manger par un de ses "collègue" durant la période où ils ne sont pas surveillés ?
(Le loup mange la chevre et la chevre mange le chou.)
Indice 1
Indice 2
- Réponse
0) Situation de départ. Loup+Chèvre+Choux+Fermier~~~
1) Il traverse avec la chèvre. Loup+Choux~~~Chèvre+Fermier
2) Il revient à vide. Loup+Choux+Fermier~~~Chèvre
3) Il traverse avec le loup. Choux~~~Chèvre+Loup+Fermier
4) Il revient avec la chèvre. Chèvre+Choux+Fermier~~~Loup
5) Il traverse avec le choux. Chèvre~~~Loup+Choux+Fermier
6) Il revient à vide. Chèvre+Fermier~~~Loup+Choux
7) Il traverse avec la chèvre. ~~~Loup+Chèvre+Choux+Fermier
Des maillons
Sachant qu'il en coûte 50 frs pour briser un maillon, et 100 frs pour le souder,
quel est le moyen le moins cher pour former une chaine fermée (qui forme une boucle) avec les 4 morceaux ci-dessous, et combien celà coûtera t-il ?
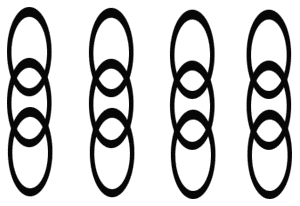
- Réponse
Briser le maillon du milieu de la 1ère chaine. (50f)
(On obtient donc 3 maillons libres, dont 1 brisé et 2 entiers, et 3 chaînes de 3 maillons.)
Briser (50f) l'un des maillons libres entiers et le glisser entre deux chaines, et ressouder ce maillon (100f).
(On a à présent deux maillons libres, l'un brisé et l'autre entier, une grande chaîne de 7 maillons et une petite de 3 maillons.)
Briser (50f) le maillon libre entier et le glisser entre la grande chaîne et la petite chaîne, puis ressouder ce maillon (100f).
(On obtient donc une grande chaîne de 11 maillons et il nous reste un maillon libre brisé).
Passer le maillon libre brisé dans chacune des extrémités de la grande chaîne, puis le ressouder (100f).
Voilà ! On obtient une unique chaîne fermée de 12 maillons, pour un total de 450f.
(Merci Pulpe)
Dessines-moi une maison.
D'un seul trait, sans jamais lever le crayon et sans repasser 2 fois au même endroit, essayez de reproduire ces dessins:
Commencons par quelques choses de faciles:
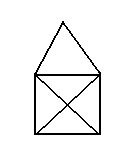
- Réponse
On part d'en bas à droite, on monte, on fait la pointe, on descend, on monte la diagonale, on traverse en haut, on descend en diagonale, on traverse en bas.
Il y a bien sûr d'autres solutions symétriques ou dans un autre sens.
Dessines-moi une maison 2.
Un peu plus dur:
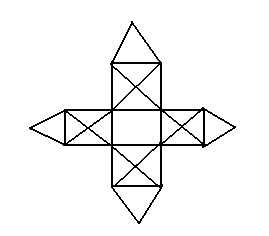
- Réponse
-
Faire 4 fois à la chaîne comme pour maison 1.
Commencer par dessiner le contour.
Une fois le tout relié, réaliser les croix que vous reliez par le segment "soutien du toit": la base de chaque pyramide.
Après avoir dessiner chaque croix et chaque base de pyramide, il ne vous reste plus qu'à dessiner le carré central.
Voilà !!
(Merci Sebii57390)
Dessines-moi une maison 3.
Bonne chance:
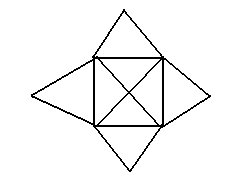
Indice 1
- Réponse
Il n'y a aucune solution (sauf en pliant la feuille - merci Soumonné).
Démonstration reposant sur la théorie des graphes:
Le problème revient en fait à chercher une chaîne eulérienne dans le graphe associé au dessin,
(les intersections sont les sommets, et les traits les reliant sont les arêtes).
Une chaîne eulérienne est en effet un chemin passant par toutes les arêtes une et une seule fois.
Or si l'on a une chaîne eulérienne, tous les sommets sauf éventuellement ceux de départ et d'arrivé sont
de dégré pair (le nombre d'arête relié à ces sommets est pair).
Donc comme ici on a 4 sommets de degré impair (les quatres coins du carré sont de degré 5), il ne peut y avoir de chemin eulérien.
(La démonstration de la propriété des chaînes eulériennes utilisée ici peut ce faire par récurrence sur le nombre d'arêtes).
Démonstration algorithmique:
Partir du milieu d'un segment ne présente aucun avantage puisqu'il faudra revenir sur le même segment à la fin,
il faut donc partir d'une intersection de segments.
Les pointes peuvent être vu comme un seul segment.
On numérote ainsi les intersections en violet et les segments en noir:
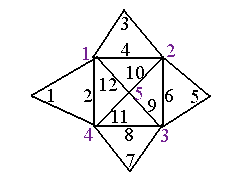
Il ne reste donc "qu'à" partir de chacune des cinq intersections en essayant tous les chemins possibles,
sans repasser deux fois sur le même segment.
Le faire à la main est difficile (enfin surtout très long), mais en utilisant un algorithme récursif on peut le faire assez facilement et constater qu'il n'y a aucune solution.
Le porte-a-faux
On empile des morceaux de sucre identiques selon leur face ayant la plus grande surface.
Est-il possible en les décalant progressivement d'obtenir un porte-a-faux de longueur infini ?
Autre énoncé :
Un bambin qui joue aux Lego se propose en utilisant des briques identiques de construire un tremplin pour franchir une riviere.
La base du tremplin est une brique unique.
Y arrivera t-il ?
Indice 1
Indice 2
Indice 3
- Réponse
Oui, c'est possible, par contre la hauteur augmente très vite.
Voici une explication plus complète : http://math.pc.vh.free.fr/divers/paradoxes/dominos.htm.
(Merci Vinhly)
Les salades
Un paysan possède 10 salades.
Il décide de les planter de manière à obtenir 5 rangées de 4 salades.
Comment va-t-il s'y prendre ?
Indice 1
Indice 2
Indice 3
- Réponse
-
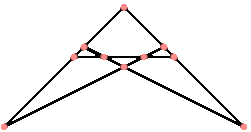
(Merci Zik-love)
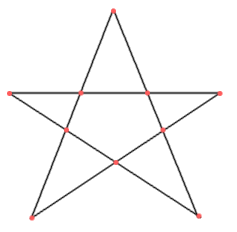
(Merci Zik-love)
Une suite de symboles
Compléter la suite de symboles suivante :

Indice 1
Indice 2
Indice 3
- Réponse
C'est le symétrique de F et F collé qui doivent suivre.
Suite de symboles
Quelle est la figure qui devrait suivre dans cette séquence ?
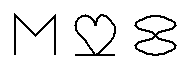
- Réponse
C'est le symétrique de 4 et 4 collé qui doivent suivre.
Verres et pièces
Vous disposez de 3 verres sur une table et de 11 pièces de monnaie.
Disposez les pieces de telle manière à ce qu'il y ait un nombre impair de pièces dans chaque verre.
OK ?
Maintenant faites-la même chose avec 10 pieces...
Indice 1
Indice 2
Indice 3
- Réponse
Pour 11 par exemple: 5 ; 3 et 3
Pour 10 par exemple: 7 dans un verre et 3 dans les deux autres emboîtés l'un dans l'autre.
Les verres
6 verres sont alignés.
Les 3 premiers sont remplis et les 3 derniers sont vides.
En ne déplacant qu'un seul verre, pouvez-vous faire alterner les verres vides avec les verres pleins ?
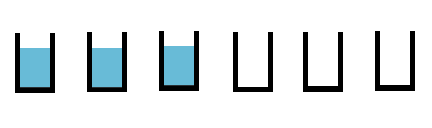
- Réponse
Prendre le deuxième verre et le vider dans le cinquième, puis le remettre à sa place.
Des vignes
Un vigneron veut planter ses 12 pieds de vignes de manière à obtenir 6 rangées de 4 plants.
Comment peut-il bien faire ?
Indice 1
Indice 2
Indice 3
- Réponse
-
Pour ce faire, il faut faire une sorte de " H " mais en mettant deux barres au milieu
au lieu d'en mettre une seule comme dans un " H ".
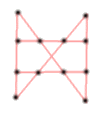
(Merci Sankaze)
Il faut faire une étoile à 6 branches (deux triangles tête-bêche).
(Merci Tom103)

