Problèmes pratiques
Partage
La pizza
Prenez une pizza et placez-la devant vous.
Vous pouvez faire uniquement 6 coupes verticales rectilignes.
Vous n'avez pas le droit de déplacer la pizza où les morceaux coupés.
En combien de morceaux au maximum pouvez-vous la détailler ?
Bonus : Pouvez-vous généralisez la solution à n coupes ?
Indice 1
Indice 2
Indice 3
- Réponse
On peut faire 22 morceaux.
Il faut qu'aucune des 6 droites représentant les coupes ne soit parallèle à une autre.
Il faut que toutes les intersections entre les droites soient strictement à l'intérieur du cercle représentant la pizza.
Il faut qu'aucune intersection ne soit commune à trois droites.
En réalité en traçant 6 droites vraiment au hasard puis un cercle tel que toutes les intersections soient à l'intérieur on trouvera ce résultat.
Voici un exemple de tracé possible (dans lesquel on distingue facilement tous les morceaux) :
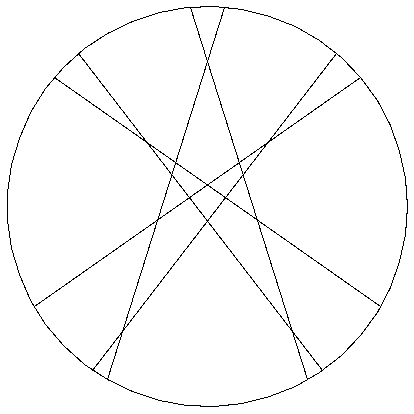
En voyant le cercle comme un cadran avec 360 points répartis sur la circonférence on a tracé :
entre 355 et 150; entre 5 et 210; entre 40 et 215; entre 320 et 145; entre 50 et 240 et entre 310 et 120.
Remarque :
Pour les 16 morceaux avec 5 coupes évoqué dans l'indice on peut faire une jolie solution :
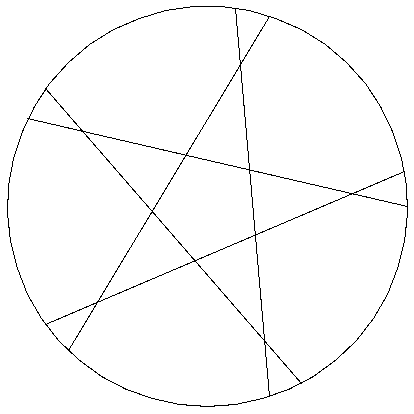
Généralisation :
Avec n coupes rectilignes on pourra faire 1+n/2+n²/2 morceaux.
En effet la nième coupe rajoute n morceaux en coupant n-1 droites plus les bords du cercle.
On a ainsi une suite : u(0) = 1 et u(n) = u(n-1) + n.
D'où u(n) = 1 + somme de i pour i allant de 1 à n,
donc u(n) = 1 + n * (1+n)/2 = 1 + n/2 + n²/2
La solution pour 6 coupes ci-dessous permet de généraliser facilement la construction d'une solution pour n coupes :
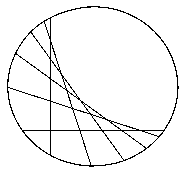
Partage de vaches
Un fermier possède 17 vaches.
Il veut donner:
1/9 à son premier fils
1/3 à son second fils
1/2 à son troisième fils.
Comment y parvenir et garder les vaches vivantes.
Indice 1
Indice 2
Indice 3
- Réponse
S'il en avait 18 cela ferait 18/9=2 18/3=6 et 18/2=9 or 2+6+9=17
donc il n'a qu'à faire comme s'il en avait 18.
Il en donne 2 au premier fils, 6 au second, 9 au dernier.
(l'astuce est que 1/9 + 1/3 + 1/2 = 17/18 est plus petit que 1.)
Terrain circulaire
Vous possédez le terrain suivant:
Vous devez le partager en 2 parties égales et ayant chacunes le même périmètre que le terrain initial.
- Réponse
Il faut faire deux demi-cercles à la manière du symbole représentant le yin et le yang.

Ainsi, un demi-périmètre du grand cercle de rayon r = 2 demi-périmètre des petits cercle de rayon r/2.
En effet (1/2)*(2*pi*r) = 2*((1/2)*(2*pi*(r/2))).
Couper un gâteau
Comment couper un gâteau en 8 parts en 3 coups de couteau ?
(Evidemment chaque coupe est rectiligne et traverse le gateau d'un bout à l'autre.)
Indice 1
Indice 2
Indice 3
- Réponse
-
Le couper en quatre verticalement (+), puis le couper horizontalement (dans l'épaisseur) pour faire 8 part.
Le couper en 4.
On emboite les 4 parts les unes sur les autres.
On coupe le tout en 2 en un seul coup.
(Merci Chfab et Kos)

